导读
作者：何 雪，杜 波，刘兆辉，杨 样，万莲娟，夏元友 ( 重庆红宇精密工业集团有限公司，重庆 402760)
来源：《工程与试验》2024年3月
摘要：针对工程实际中广泛采用的螺纹紧固联接结构紧固力矩设计困难的问题，结合预紧力与紧固力矩关系，设计典型结构开展了不同长度螺钉、不同材质连接工件的扭力试验，获取了设计结构下的屈服扭矩、失效扭矩、失效转角等重要数据。根据屈服扭矩和螺钉力学性能，获取了螺钉与典型表面处理后工件接触支撑面摩擦系数，此试验方法可实现螺纹紧固联接结构的快速设计，提高设计效率和实现工程应用。
一、引言
螺纹紧固广泛应用于机械结构连接，特别是反复拆卸的机械结构。螺纹联接时，为了达到可靠而紧固的目的，必须保证连接工件具有一定的摩擦力矩，此摩擦力矩是由连接时施加拧紧力矩后，螺纹副产生了预紧力而获得。预紧力过大或过小都会使螺纹联接失效，过小的预紧力会使得螺纹副连接在振动冲击环境中松动脱落，过大的预紧力会使得螺牙塑性变形( 滑丝)［1］。在螺纹紧固件标准中给出了预紧扭矩与预紧力的关系，以及标准螺纹不同摩擦系数下的紧固系数。而摩擦系数影响因素较多，包括表面粗糙度、表面处理方式等［2］。行业内并无明确的螺纹安装扭力查询手册，在实际使用中，会查询到螺纹的推荐使用扭矩值或螺钉生产厂家给定的建议扭矩值，但是由于工况不一样，连接件的材料不一样，连接件的粗糙度及表面处理方式不一样，往往不能直接使用推荐值。
为了得到可靠的螺纹联接结构，目前业内多采用典型结构试验，得到特定工况下的螺纹可靠紧固扭矩，再用扭力旋具进行扭力控制，以达到螺纹可靠联接的目的。但航空、航天、船舶等领域螺纹联接较多，开展试验工作量大; 空间受限，不便于使用扭力旋具; 多为单件、小批量生产，花费大量时间、人力、物力进行典型结构的螺纹扭力试验，经济效益不高。在实际应用中，针对典型结构开展螺纹紧固扭力试验， 得到特定螺纹在典型结构下扭力与转角的关系［3］，找到规律，可以快速确定螺纹可靠联接所需的转角。在实际运用中，通过控制螺纹旋紧转角来控制螺纹联接的可靠性更具操作性，对操作人员的技能要求不严格，能很好实现工程应用。
二、预紧力与紧固扭矩关系
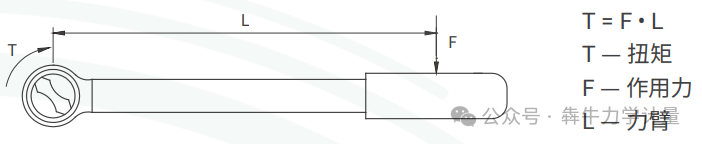
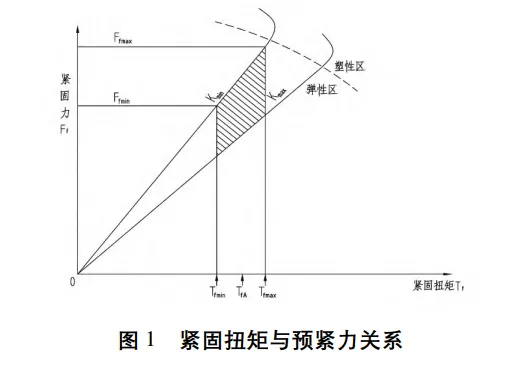
如图 1 所示，在弹性阶段，紧固扭矩与预紧力成线性关系［4］。紧固扭矩与预紧力的关系如下［5］:
Tf = KFfd ( 1)
式中，Tf 为紧固扭矩，Ff 为预紧力，K 为紧固系数，d 为 螺纹公称直径。
式( 1) 中，紧固系数计算公式为: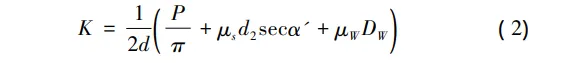
式中，P为螺距，μs为螺纹副摩擦系数，μW 为支撑面摩擦系数，DW为支撑面摩擦扭矩等效直径，α' 为螺纹牙侧角， tanα' = tanαcosβ ，α 为螺纹牙型角，β 为螺纹升角。 在紧固过程中，螺钉承受预紧力产生的正应力及螺纹扭矩产生的剪应力。
正应力［5］:
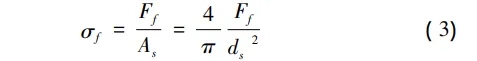剪应力［5］:
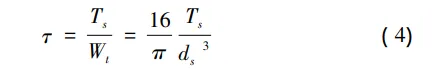预紧力与螺纹扭矩有如下关系［1］:
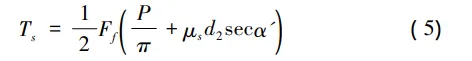式中，d2为螺纹中径，ds为标准有效截面直径，μs为螺纹副摩擦系数。按第四强度理论，螺钉屈服紧固轴力为［5］:
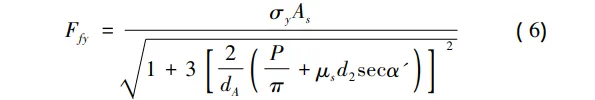式中，As 为应力截面积，dA 为等效直径。 与屈服紧固轴力对应的屈服紧固扭矩为［5］:
Tfy = KFfyd ( 7)
三、扭力试验与结果分析
3. 1 不同旋合长度扭力试验
3. 1. 1 试件
试验螺钉 为 8. 8 级 M6 六角头标准螺钉，长 10mm、12mm、15mm; 通孔连接件材料为2A12 铝合金，内螺纹连接件材料为45#钢板，热处理硬度28HＲC～ 33HＲC。通孔连接件简称试件1－1，内螺纹连接件简称试件1－2，试验连接件如图 2 所示。
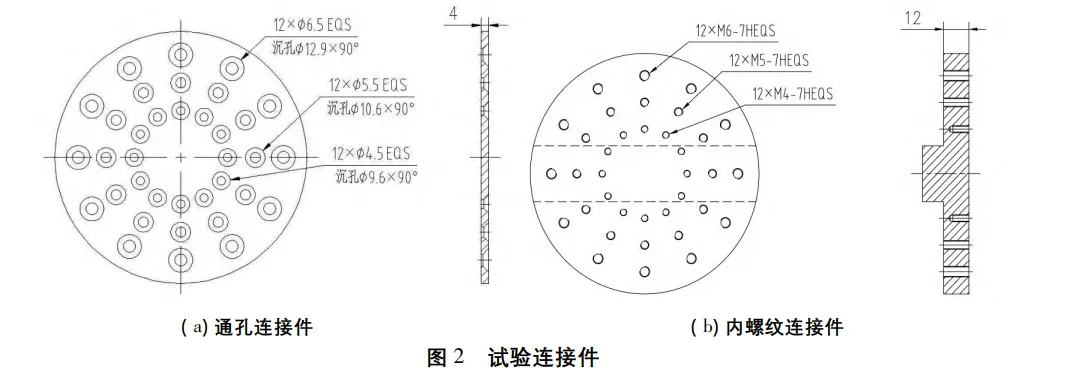试件 1－2 上，用扭力扳手拧紧。拧转螺钉过程中，保持拧转力矩方向垂直于螺钉旋入方向，速度均匀而慢，用力平稳，不可使用冲击力［6］。 采用扭力扳手记录紧固扭矩值，用自制带刻度的分度盘读取转角度数［7］，在螺钉拧到位开始预紧［8］( 即拧紧扭矩开 始明显增加) 时，每 5°转角记录一次扭矩，同一螺钉及状态进行重复试验，绘制曲线。
3. 1. 2 试验结果
对 3 种长度的螺钉施加紧固扭矩，直至螺钉失效。测试结果见表1，绘制的扭矩－转角曲线如图3 所示。
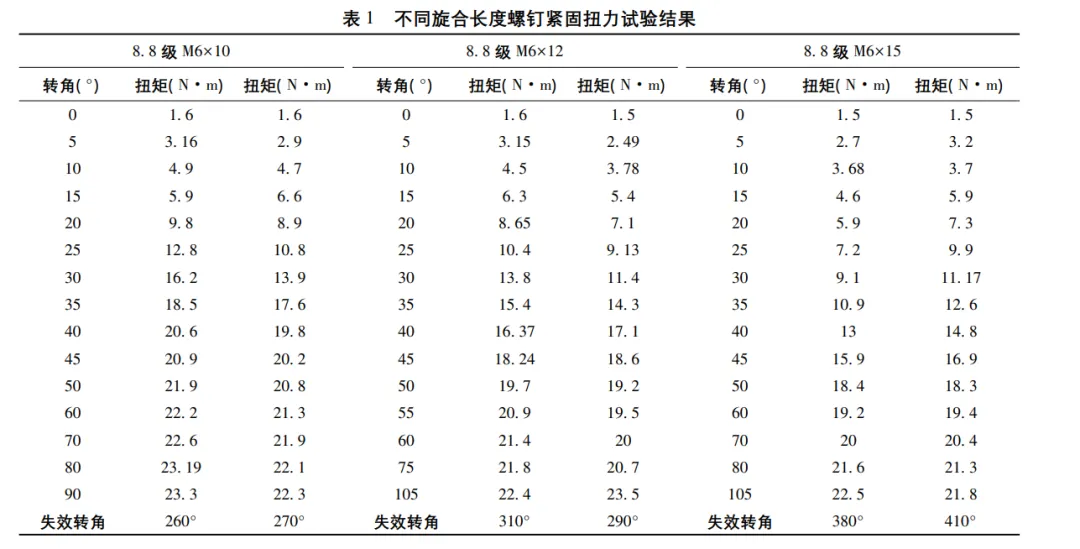
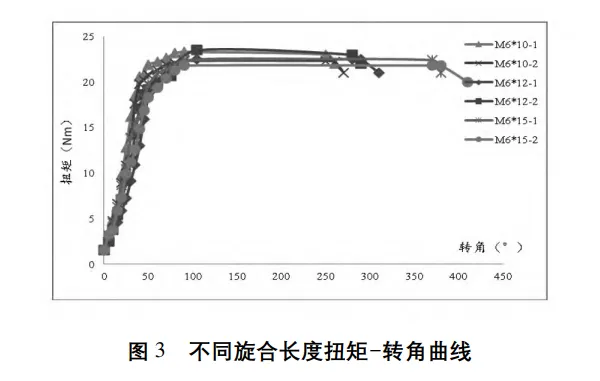
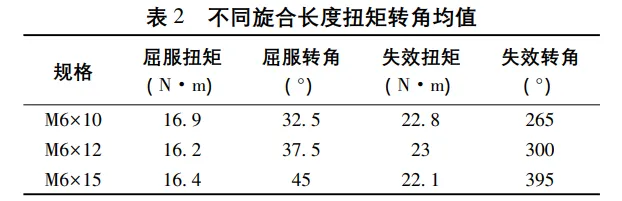
不同旋合长度扭矩转角均值见表 2，由试验数据可以看出，不同长度螺钉的屈服扭矩与极限扭矩相当; 螺钉越长，极限扭转角越大。
M6 标准粗牙螺钉参数: P = 1mm，d2 = 5. 35mm，As = 20. 1mm2 ，dw = 8. 73mm，按照规范建议螺纹副摩擦系数取 μs = 0. 14，代入式( 6) ，得到屈服预紧力，再以试验屈服扭矩代入式( 7) ，得到支撑面摩擦系数 μW = 0. 26。通过计算和数据处理，得到不同旋合长度紧固扭矩计算值与试验值，如表 3 所示。采用式( 2) 进行紧固系数计算，发现失效扭矩试验值比计算值略大。
3. 2 加垫圈扭力试验
3. 2. 1 试件
测试螺钉为12. 9 级 M5 标准六角头螺钉，连接内螺纹件材料为45#钢，表面镀锌镍合金，通孔件材料为 2A12 铝合金。
3. 2. 2 试验结果
无垫圈状态下，铝合金与螺钉接触表面有明显的压痕和黏着痕迹，带垫圈后无明显压痕，测试结果如表 4 所示。
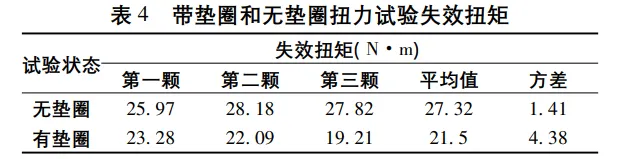
M5 标准粗牙螺钉参数: P = 0. 8mm，d2 = 4. 48mm，As = 14. 2mm2［4］。摩擦系数 μs = 0. 14、μW = 0. 26，通过计算和数据处理，得到带垫圈和无垫圈扭力试验失效力矩计算值与试验值，见表5。可以看出，有垫圈状态下，紧固失效扭矩试验值比计算值略大; 无垫圈状态下，试验扭矩值明显大于计算值。由此可见，高强度螺钉连接低刚度和高强度工件时，螺钉与接触表面发生黏着现象［9］，摩擦力增加，从而使得扭矩增加，导致在同样的扭矩下得不到预期的预紧效果［10］。在实际操作中，应避免高强度螺钉与低强度工件直接接触，可采用垫圈的形式优化设计。
3. 3 不同材质和表面处理连接件扭力试验
3. 3. 1 试件
试验螺钉采用6. 8 级 M6×15 六角头标准粗牙螺钉，连 接件分别为: 20#钢镀锌镍合金，45#钢镀锌镍合金，45#钢淬火硬度 38HＲC～ 43HＲC 镀锌镍合金，2A12铝合金，2A12铝合金阳极氧化，30CrMnSiNi2A合金钢镀锌镍合金， 30CrMnSiNi2A 合金钢淬火硬度 28HＲC ～ 33HＲ镀锌镍合金， 30CrMnSiNi2A合金钢淬火硬度 38HＲC～ 43HＲC镀锌镍合金。装夹、测试记录和过程要求同上文。
3. 3. 2 试验结果
对不同材质及表面处理连接件进行紧固扭矩试验，测试 结果见表 6－表 11，典型试验如图 4 所示。将试验数据绘图 可得扭矩－转角曲线［11］，不同材质连接件扭矩－转角曲线如 图 5 所示。
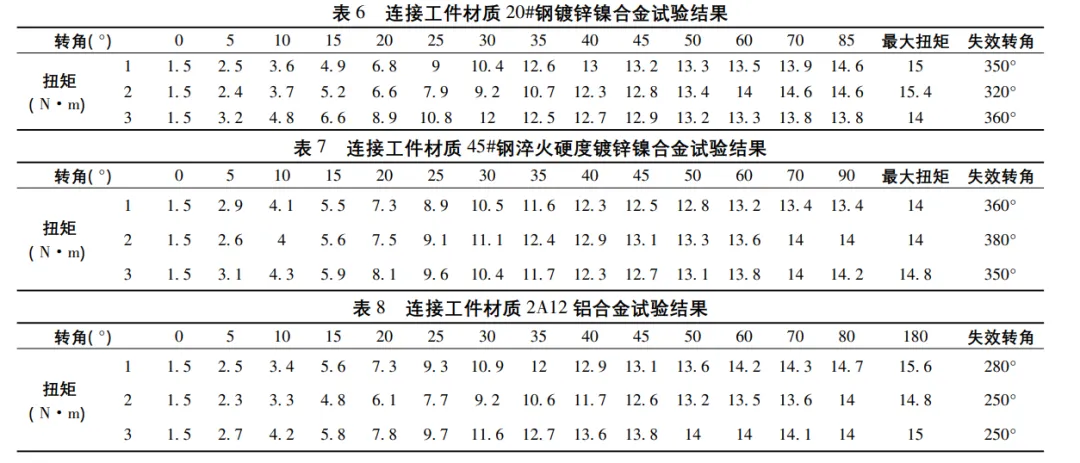
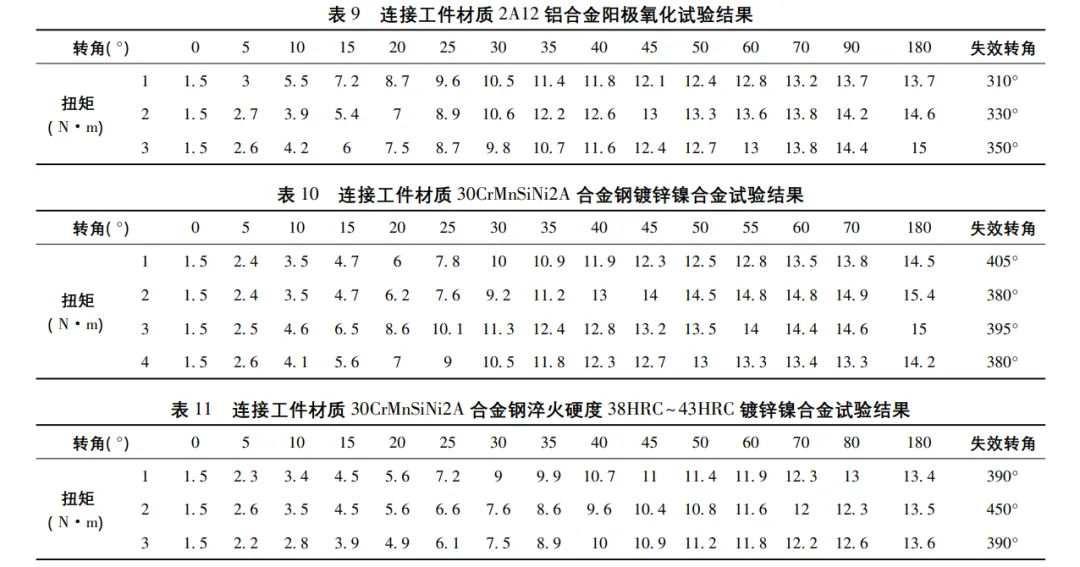
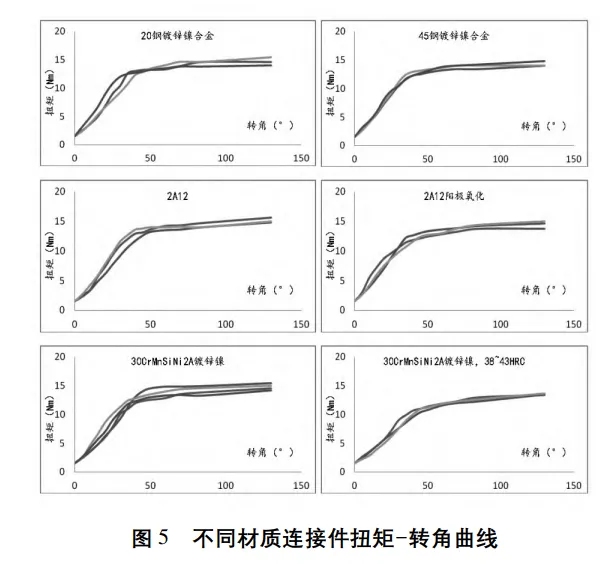
不同材质连接件的屈服扭矩和失效扭矩典型值统计结果如表12所示，可以看出，20#钢、45#钢、30CrMnSiNi2A 合金钢表面镀锌镍合金后作为连接件开展螺纹扭力试验，其屈服扭矩及失效扭矩相近，没有明显差异; 对于 2A12 铝合金，经阳极氧化处理后作为连接件开展螺纹扭力试验，其屈服扭矩略有减小; 对于表面镀锌镍合金的 30CrMnSiNi2A合金钢连接件，表面热处理后作为连接件开展螺纹扭力试验，其屈服扭矩减小
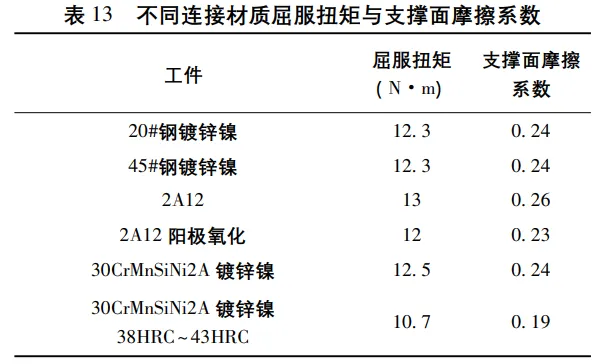
M6标准粗牙螺钉参数及螺纹副摩擦系数取值同上文，代入式( 6) 得到屈服预紧力，再以试验屈服扭矩代入式( 7) ， 反算求得支撑面摩擦系数，相关计算值见表13。20#钢、45# 钢、30CrMnSiNi2A 合金钢表面镀锌镍后，支撑面摩擦系数约为0.24，经淬火硬化后，摩擦系数降为0.19。2A12 铝合金表面未经阳极氧化处理时，支撑面摩擦系数约为0.26，经阳极氧化处理后，支撑面摩擦系数约为0.23。
由图5可以发现，在使用M6×15螺钉的情况下，不同材质连接件扭矩趋于平稳时的转角值几乎一致，均在60°时趋于平稳。从图3可以看出，使用不同长度M6螺钉连接同状态连接件时，转角值几乎一致，均在60°时趋于平稳，即根据业内经验取 42°( 60°×70%) 作为可靠转角。
四、结论
( 1) 不同长度螺钉屈服扭矩与极限扭矩相当，螺钉越长，极限扭转角越大。
( 2) 失效扭矩试验值比理论计算值略大。
( 3) 在有垫圈状态下，紧固失效扭矩试验值比理论计算值略大。
( 4) 高强度螺钉与低强度工件直接接触时，即无垫圈状态下，紧固失效扭矩试验值明显大于理论计算值，故应避免高强度螺钉与低强度工件直接接触。
( 5) 20#钢、45#钢、30CrMnSiNi2A 合金钢表面镀锌镍合金后作为连接件，其屈服扭矩和失效扭矩相近，没有明显差异。对于2A12铝合金，经阳极氧化处理后作为连接件，其屈服扭矩较非阳极氧化件略有减小。对于30CrMnSiNi2A 合金钢淬火硬化后作为连接件，其屈服扭矩减小。
( 6) 20#钢、45#钢、30CrMnSiNi2A 合金钢表面镀锌镍后，支撑面摩擦系数约为0.24，经热处理硬化后，摩擦系数降为0.19; 2A12 铝合金表面未经处理时，支撑面摩擦系数约为0.26，经阳极氧化处理后，支撑面摩擦系数约为0.23。
( 7) 使用不同螺纹长度的 M6 螺钉连接常用的 20#钢、45#钢、30CrMnSiNi2A合金钢、2A12 铝合金( 带垫圈) 作为连接件的情况下，均可选取 42°作为可靠转角。
( 8) 指定规格的螺纹，在避免高强度与低强度材料直接连接的情况外，安装可靠转角与螺纹长度、连接件材料为弱相关。
五、参考文献
［1］倪晋挺．螺纹紧固件摩擦系数的影响因素试验研究［J］．黑龙江工程学院学报，2016，30( 3) : 26-28，32．
［2］尚红旗．螺纹紧固件扭矩系数影响因素分析［J］．科技创新与应用，2016( 5) : 129-129．
［3］马贝方，陈智隆，于乐翔，等．螺纹紧固件拧紧过程角度监控和扭矩监控研究［J］．汽车实用技术，2021，46( 24) : 109-113．
［4］中国机械工业标准汇编．紧固件基础卷［S］．北京: 中国标准出版社，1997．
［5］山本晃．螺纹联接的理论与计算［M］．上海: 上海科学技术文献出版社，1984．
［6］樊水晶，高颖阁，程芝群．机械设计中螺纹防松方法的探讨［J］．科技创新与应用，2019( 8) : 110-111．
［7］李斌，董彬，李志强．汽车螺纹紧固扭矩与检验扭矩关系验证［J］．汽车工程师，2011( 5) : 43-45，62．
［8］陈伟婧．螺纹连接松动机理及防松技术研究［J］．科学技术创新，2022( 30) : 175-179．
［9］张守阳，赵兵，倪红军，等．航空螺纹紧固件扭矩系数变化规律的试验研究［J］．组合机床与自动化加工技术，2020( 9) : 25-28．
［10］韦小华，徐清魁．浅析螺纹紧固件扭矩的计算与验证［J］．汽车实用技术，2021，46( 18) : 137-140，166．
［11］陈德安．几何偏差下螺栓预紧力和残余扭矩形成机理的研究［D］．辽宁: 大连理工大学，2019．
文章来源于网络，版权归原作者所有，侵删。
